“广义相对论的钥匙:张量”专题之三
“张量”是广义相对论的钥匙,用来表示与坐标无关的量。
之前的章节:
上一节,我们研究了向量空间以及其中的向量:
向量空间的基和向量都是张量:
下面来介绍线性代数中另外一个重要组成部分,余向量以及对偶空间。
1.1 什么是余向量(covector)?
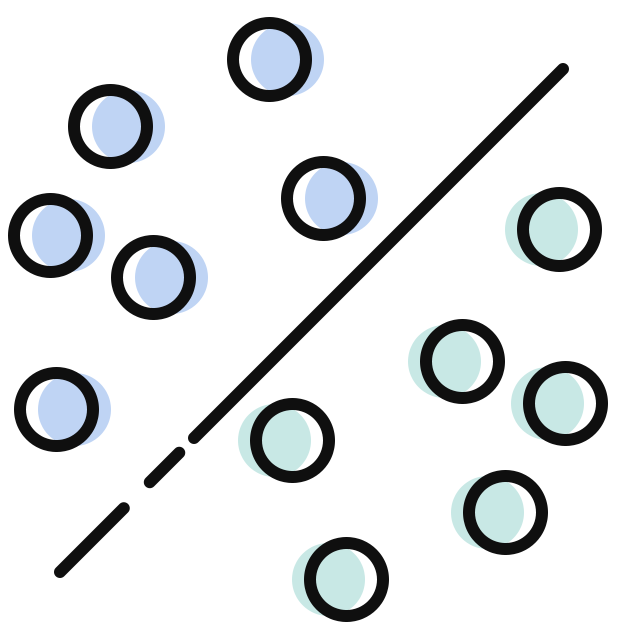
空间中的直线、平面这些“线性”的几何对象,也是线性代数所关心的。
比如平面中的一条直线,很显然与坐标无关,是一个几何对象:
此直线在不同的基下有不同的代数表示:
直线符合之前说的张量的特点:
-
直线是一个几何对象,它与基无关
-
不同的基下,有不同的代数表达
-
并且,不同的坐标值之间有明确的转换规则
表示直线、平面这些“线性”的几何对象的就是余向量,也是张量的一种。
1.2 余向量的细节
刚才的直线,在直角坐标系下:
对应的直线方程为:
在正交单位基下,可以用这个式子来表示:
此处,可认为行向量
更严格来说,应该把余向量看作表示这根直线的线性函数:
给行向量一个符号:
那么,这样表示看着是不是更像函数:
值得注意的是,余向量是
实际上,它代表了所有平行的直线。
写成线性函数的样子就是这样的:
1.3 余向量的几何表示方法
介绍一下余向量的几何表示方法,还是拿余向量
提醒一下,
余向量表示的是一系列平行的直线,所以把这些平行的直线都画出来(为了不显得太乱,只画出单位正交基,不画出网格了):
下面和右面标出的数字指明了是哪一根直线,比如:
上图数字6对应的就是下面这根直线:
如果有某个向量和其中一根直线相交,比如:
向量
这样的几何表示方法可以帮助后面更好的理解和展示余向量。
2.1 余向量的线性组合
我们来定义一下余向量的:
-
数乘:
-
加法:
其中
这样定义是合理的、自洽的,用具体的值来试算一下,令:
数乘:
加法:
从几何直观来看,
而
而
可以认为这根直线是之前两根直线的线性组合。
2.2 对偶空间
向量空间定义是这样的:
设
所谓封闭,是指在
-
若
,则 -
若
,则
也就是说,向量空间
同样的道理,有个数乘和加法之后就可以定义对偶空间了。
对于余向量的数乘和加法封闭的空间,称为对偶空间,一般记为
3.1 余向量的基
对于向量而言:
首先要把向量用基来表示,才能去讨论如何进行坐标转换:
所以要谈论余向量在不同坐标下的表示:
首先要定义出余向量的基。
说来也简单,定义这样一个线性函数作为余向量的基(余向量的基用的是上标,也就是说它是逆变量,这个后面再解释):
上面用
这样的定义也不难理解,对于单位正交基下的余向量
验算一下:
可见,这样的定义是符合直觉的。之前我们的余向量也可以用基的线性组合来表示:
为了更方便记忆,引入一个函数,可见我们只需要关心
来看下这两个基的几何表示(标出
另外一个基:
余向量用基的线性组合来表示:
上面是用单位正交基来举的例子,后面我用代数推一下,证明余向量可以被基线性表示。
3.2 余向量的基作用在向量上
先来算一下,余向量的基和向量之间的计算结果是什么?
同理:
看来,余向量的基有把坐标的分量分离出来的作用:
这点从几何上也可以看出,比如,这个向量与
与
上面这个向量确实就是:
3.3 余向量通过基来表示
把之前的余向量用符号来表示:
看看它是怎么作用到向量上的:
令:
其中,
并且根据刚才的结论:
所以上式可以变为:
可见余向量可以由余向量的基来线性表示:
其中:
3.4 小结
停顿下,至此,得到了下面这些结论,注意,虽然上面举例子画图用的是单位正交基,但是下面的结论对所有基都成立。
余向量的基的定义:
余向量与向量之间的作用:
余向量用基来表示(用了爱因斯塔标记法,把
其中:
终于做好准备了,让我们看看在不同基下余向量应该怎么转换吧。
4.1 明确目标
用实际的例子进行说明,在这两个基下,余向量应该怎么表示:
上图中的左边的基就是单位正交基,代数形式为:
上图中的右边的基为:
两个基的转换图为:
转换矩阵具体是:
4.2 余向量的转换
根据之前我们得出的结论:
其中:
可知,余向量的坐标可以由余向量与基来决定。
根据这个结论,其实可以通过几何看出余向量是什么。比如,之前
在我们关心的另外一个基下:
从代数上这么求:
转回来可以这么算:
余向量的转换图为:
余向量的改变与向量的基改变是一致的,因此是协变量。
给一副动图,可以看出确实是协变量:
至此,可以用爱因斯塔标记法表示出余向量:
4.3 余向量的基的转换
向量的基和向量之间的转换是反的,可以这么想象,基变长了,那么要表示同一个点,坐标自然需要变小,来补偿这个变化。
同理,余向量的基和余向量之间的转换也是反的,余向量的基是逆变量:
本文介绍了什么是余向量以及余向量的基,新得到两个张量:
关注马同学

微信公众号:matongxue314