光滑曲线的长度
前面几节学习了定积分以及它的求解,并通过它定义了曲边梯形的面积。其实定积分还可以提供很多定义,还有很多的应用,本节就来学习其中一些。
定义 .若函数在区间
上有连续的导函数,那么称该函数在
上的是 光滑 的。
举例说明下,若函数符合上述定义,则其有连续的导函数,这意味着其微分的斜率是连续变化的。从几何上观察的话,如下图所示,随着切点的移动,该点的微分在顺滑地“转动”。该函数的曲线看上去也符合我们对“光滑”的直觉。
随着的移动,光滑曲线在
点的微分在顺滑地“转动”
定义 .若函数在区间
上是光滑的,那么定义该函数在
上的长度
为:
若定义 弧微分 为
,那么上式可以简写为
。
上述给出的就是光滑曲线长度的定义(不是所有的曲线都可以求长度的,不过光滑曲线是一定可以求长度的,这里不作进一步的解释),大意就是各个线段长度之和就是光滑曲线的长度,和之前的分析是一样的。下面是进一步的解释,在中任意插入若干个分点
,将
分成
个小区间,如下图所示。仔细观察函数
在小区间
上的曲线,该曲线的长度可记作弧长
。
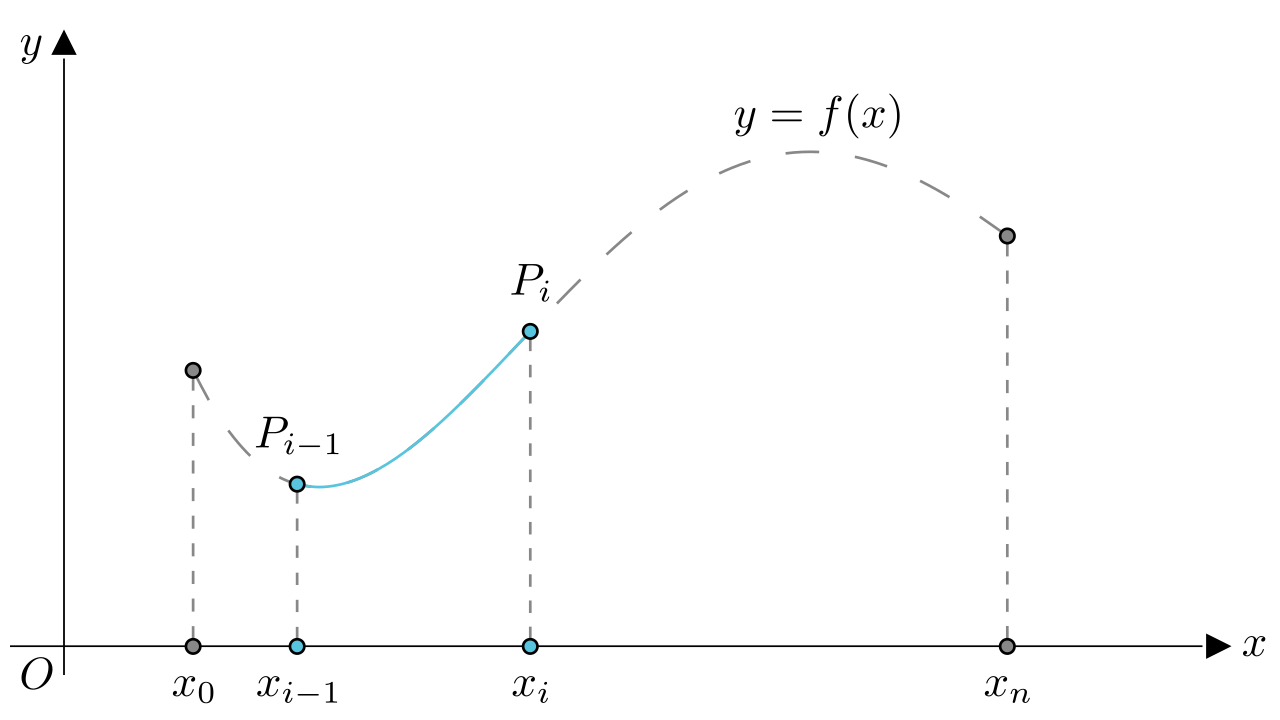
函数在小区间
上的曲线,其长度记作弧长
在区间上随便挑选一点
,作出函数
在该点的切线,如下图所示。
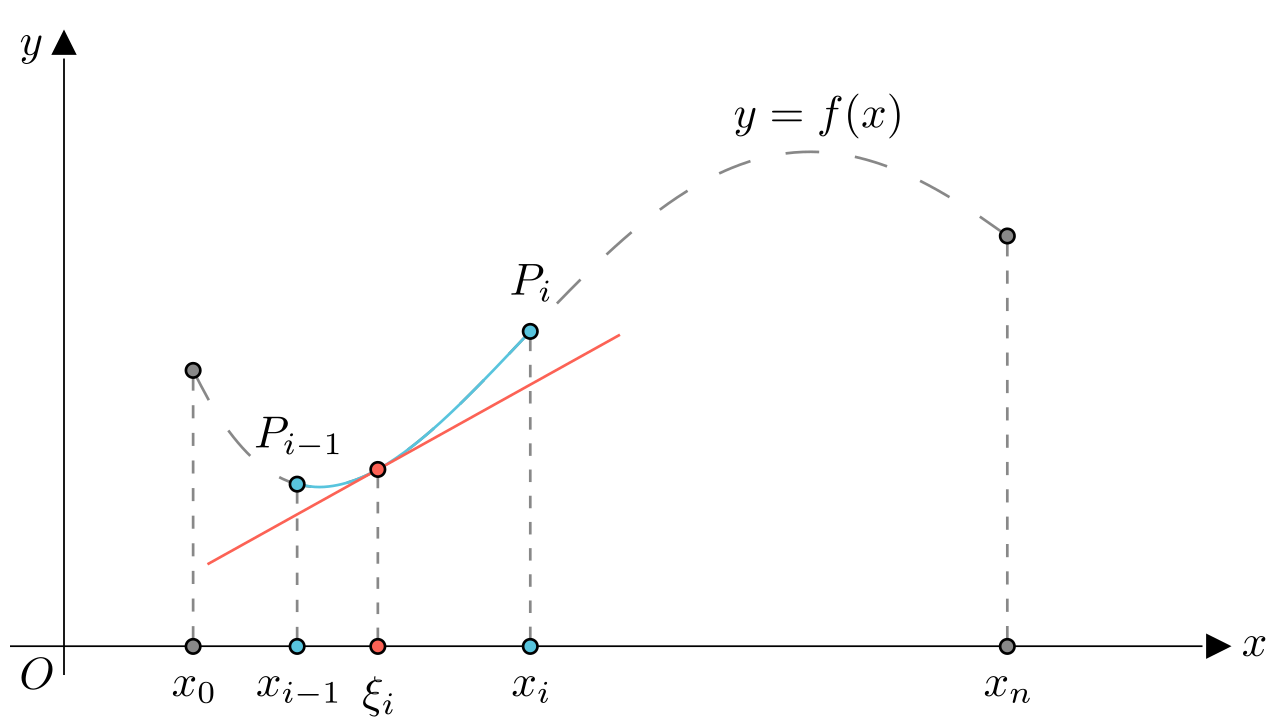
作出函数在
点的切线
按照下述规则作出直角三角形,其图像如下图所示。
- 斜边为该切线在区间
上的一段,记作
- 底边记作
,其值为
- 高记作
,因为切线的斜率为
,所以有
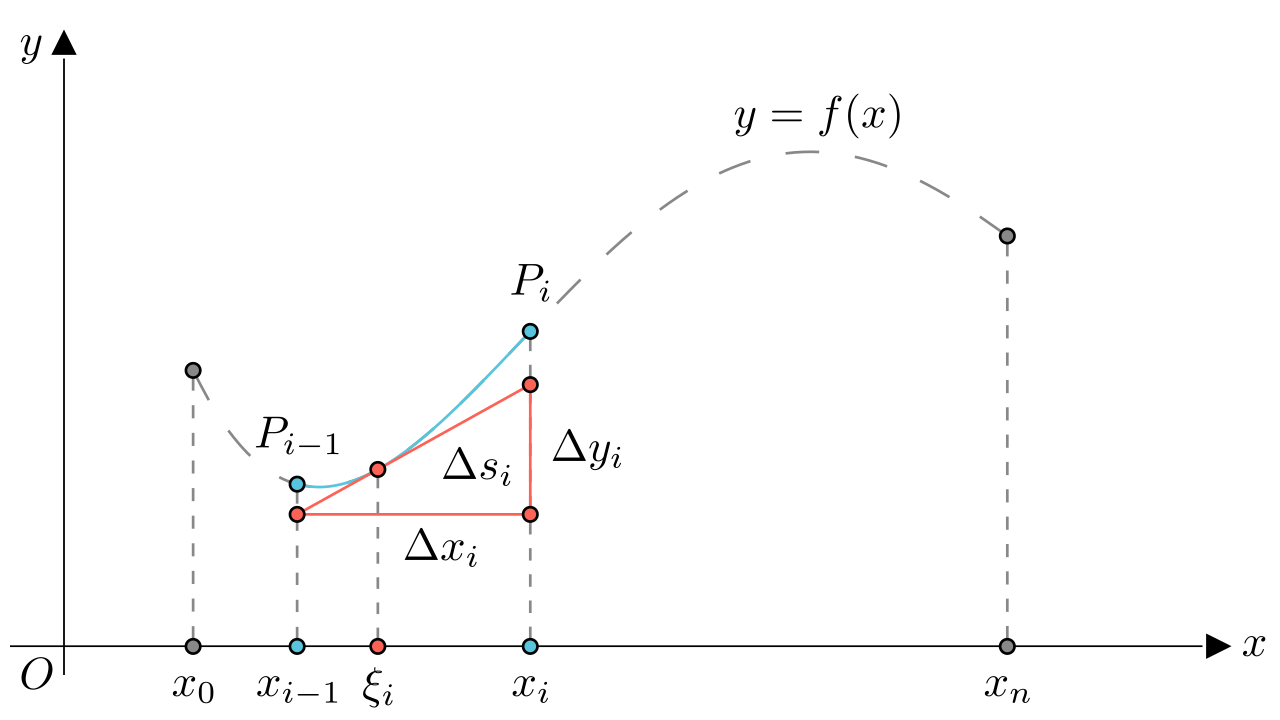
以点的切线为斜边,作出直角三角形
所以可算出斜边的长度,也就是切线段的长度如下:
根据微积分“以直代曲”的思想,可认为弧长近似等于切线段长度
,即:
记函数在
之间的曲线的长度为
,该长度可近似为如下:
令,因为函数
在区间
上连续,根据可积的充分条件 1,所以
时上述和的极限存在,并且可以直观地认为
变为了
。所以定义函数
在
之间的曲线长度
为:
其中用于近似弧线段的切线段称为该弧线段的微分,简称弧微分,记作。所以弧长公式可以理解为弧微分之(积分)和:
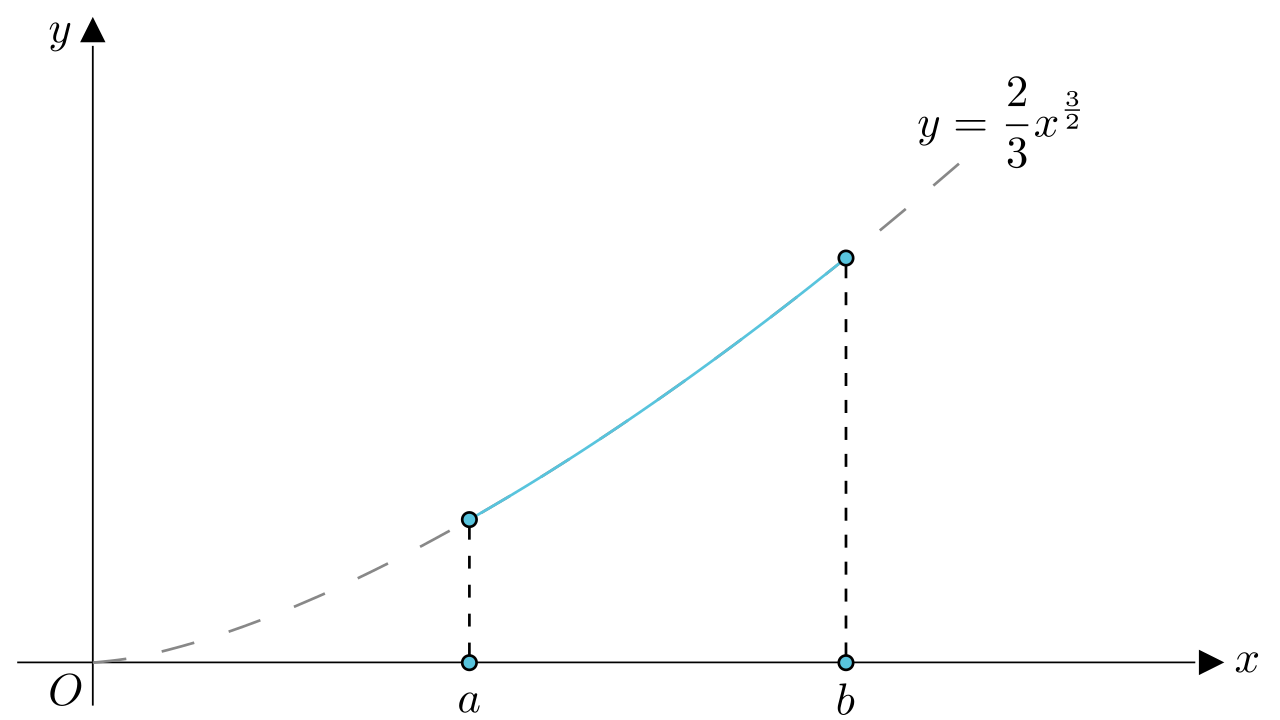
例 .请计算曲线上相应于
的一段弧的长度。
解 .下图所示的就是曲线上相应于
的一段弧。
曲线
上相应于
的一段弧
曲线
的导函数
是连续的,所以这是光滑曲线。可以先求出其弧微分:
结合上弧长的计算公式,因此所求弧长
为:
关注马同学

微信公众号:matongxue314