联合分布列

马同学

联合分布列

定义 1. 若二维随机向量 $(X,Y)$ 只取有限个或可列个数对 $(x_i,y_j)$ ，则称 $(X,Y)$ 为二维离散随机向量。
对于二维离散随机向量 $(X,Y)$ ，其联合概率质量函数，也称为联合概率函数，定义为事件 $\{X=x_i\}$ 和 $\{Y=y_j\}$ 同时发生的概率：
$p_{ij}=p(x_i,y_j)=\operatorname{P}(X=x_i,Y=y_j)=\operatorname{P}\Big(\{X=x_i\}\cap\{Y=y_j\}\Big),\quad i,j\in\{1,2,\cdots\}$
联合概率函数常写作列表的形式，这一形式也称为 $(X,Y)$ 的联合分布列：
$\begin{array}{c|ccccc} \hline \quad X\overset{\LARGE\setminus}{\phantom{.}}\overset{\Large Y}{\phantom{l}} \quad &\quad y_1\quad&\quad y_2\quad&\quad \cdots\quad&\quad y_j\quad&\quad \cdots\quad\\ \hline \\ x_1 & p_{11} & p_{12} & \cdots & p_{1j} & \cdots \\ x_2 & p_{21} & p_{22} & \cdots & p_{2j} & \cdots \\ \vdots & \vdots & \vdots & \ddots & \vdots & \ddots\\ x_i & p_{i1} & p_{i2} & \cdots & p_{ij} & \cdots \\ \vdots & \vdots & \vdots & \ddots & \vdots & \ddots\\ \\ \hline \end{array}$

说明 .同分布列，二维离散随机向量的联合分布列也需满足非负性（ $p_{ij}\ge 0$ ）和正则性（ $\sum_{i=1}^{\infty}\sum_{j=1}^{\infty}p_{ij}=1$ ）。

根据上一节的儿童生长发育情况表，可在样本空间 $S=\{\text{旺旺},\text{明杰},\text{伟强},\text{英子},\text{思敏},\text{小芳}\}$ 上定义二维离散随机向量 $(X,Y)$ ，其中 $X$ 表示身高（cm）， $Y$ 表示体重（kg）。图 1 展示了该随机向量的联合分布列，图 2 展示了该联合分布列的图像，其中水平面上的网格交点对应 $(X,Y)$ 的取值，垂直线段的高度反映了取值的概率。

$\begin{array}{c|ccc} \hline \quad X\overset{\LARGE\setminus}{\phantom{.}}\overset{\Large Y}{\phantom{l}} \quad &\quad 18\quad&\quad 20\quad&\quad 22\quad\\ \hline \\ 108 & \displaystyle\frac{1}{6} & 0 & \displaystyle\frac{1}{6} \\ 112 & \displaystyle\frac{1}{6} & \displaystyle\frac{1}{3} & 0 \\ 115 & 0 & 0 & \displaystyle\frac{1}{6} \\ \\ \hline \end{array}$

图 1 $(X,Y)$ 的联合分布列

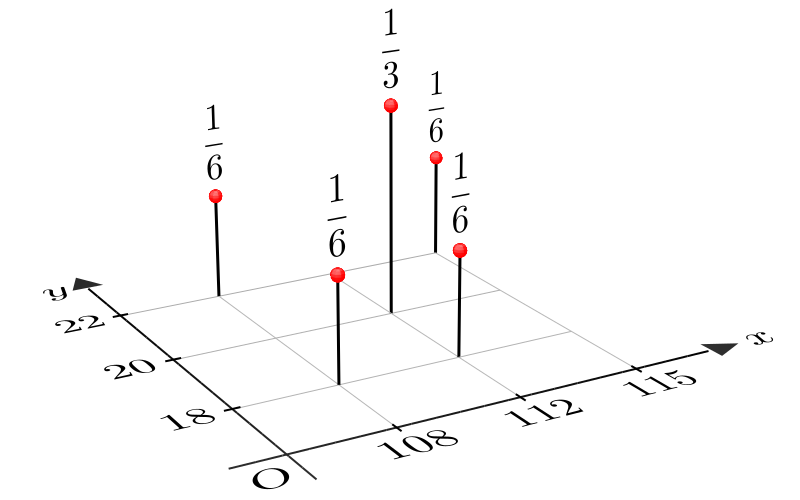
图 2联合分布列的图像

下面通过举例说明联合分布列（图 1 ）中概率的计算方法。根据生长发育表，在小区6名儿童中，身高为108cm且体重为18kg的只有"伟强"一人，因此：

$\text{“身高}\ 108\text{cm 且体重}\ 18\text{kg 的概率”}=\operatorname{P}(X=108, Y=18)=\frac{1}{6}$

而身高为112cm且体重为20kg的有“旺旺”和“英子”两人，因此：

$\text{“身高}\ 112\text{cm 且体重}\ 20\text{kg 的概率”}=\operatorname{P}(X=112, Y=20)=\frac{2}{6}=\frac{1}{3}$

从某大学食堂的就餐数据中，我们整理出了三位学生的早餐时间，如下表所示：

$\begin{array}{c|c|c|c} \hline \quad \quad &\quad \text{小明}\quad&\quad \text{小强}\quad&\quad \text{小红}\quad\\ \hline \\ \text{周一} & 6\ \text{点} & 7\ \text{点} & 6\ \text{点} \\ \text{周二} & 7\ \text{点} & 8\ \text{点} & 7\ \text{点} \\ \text{周三} & 8\ \text{点} & 6\ \text{点} & 8\ \text{点} \\ \\ \hline \end{array}$

设随机变量 $X$ 为“小明早餐时间”， $Y$ 为“小强早餐时间”， $Z$ 为“小红早餐时间”，求 $\operatorname{P}(X=6, Z=7)$ 。

$0$

$\frac{1}{3}$

关注马同学